DFS와 BFS를 학습하다가, 이 알고리즘들을 배우기 전에 이 알고리즘들의 근간을 이루고 있는 '그래프'라는 자료 구조에 대해 깊게 알아보고 가야겠다는 생각이 들었다.
✏️그래프란?
그래프란, 연결되어 있는 정점과 정점간의 관계를 표현할 수 있는 자료구조이다. [천재학습백과]
알다시피 자료구조는 크게 비선형구조와 선형구조로 구분되는데,
선형구조는 자료를 저장하고 꺼내는 것에 초점이 맞춰져 있고 (ex. 스택, 큐, 리스트, ...), 비선형구조는 '표현'에 초점이 맞춰져 있다고 생각하면 된다.
자료구조인 그래프는 바로 연결 관계에 초점이 맞춰져 있는데, 말로만 들으면 너무 추상적이게 느껴질 수 있으니 관계망을 나타내는 서비스인 페이스북으로 예시를 들어보자.
필자가 친구 "제니"를 알고 있고, "로제"와 친하다고 가정해보자.
그리고 "로제"는 에스파 "카리나"를 안다고 하면,
필자는 "카리나"와 2촌 관계라고 할 수 있는 것! (희망 사항임 아무튼 그럼)
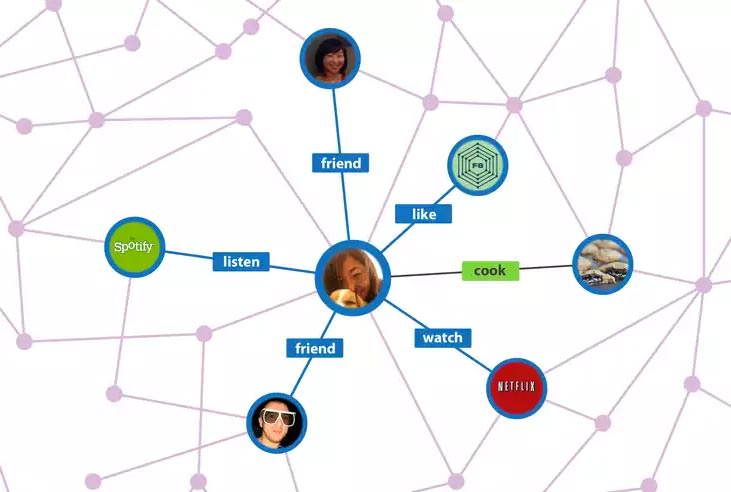
위의 그림을 보면, 어떤 누군가는 Spotify를 듣고 있고, 어떤 누군가와는 친구고, Netflix를 보고 이런 것들을 표현할 때 각각의 점들을 '노드' 또는 '정점' 이라고 한다.
그리고 노드와 노드를 잇는 선들을 '간선' 또는 '엣지' 라고 부른다.
즉, 이렇게 노드들과 간선으로 이루어진 자료 구조를 그래프라고 부른다.
💡 그래프에서 사용하는 용어 정리
노드(Node): 연결 관계를 가진 각 데이터를 의미한다. 정점(Vertex) 이라고도 한다.
간선(Edge): 노드 간의 관계를 표시한 선을 의미한다.
인접 노드(Adjacent Node): 간선으로 직접 연결된 노드(또는 정점)를 의미한다.
참고로, 그래프는 유방향 그래프와 무방향 그래프 두 가지가 있다. 말 그대로 방향이 있는 녀석과 없는 녀석이란 말인데,
유방향 그래프(Directed Graph)는 방향이 있는 간선을 갖는다. 간선은 단방향 관계를 나타내며, 각 간선은 한 방향으로만 진행 가능하다.
반면 무방향 그래프(Undirected Graph)는 방향이 없는 간선을 갖는다. (아래 사진 참고)
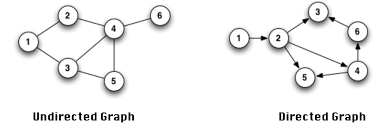
소셜 미디어 서비스를 구현할 때로 예시를 들어보면, 팔로잉 관계를 표현할 땐 유방향 그래프가 맞겠고, 그저 친구인 관계를 표현하고자 한다면 무방향 그래프가 맞겠다.
✏️그래프의 표현 방법
이런 그래프라는 개념을 컴퓨터에서 표현하는 방법은 두 가지 방법이 있다.
- 인접 행렬 (Adjacency Matrix) : 2차원 배열로 그래프의 연결 관계를 표현
- 인접 리스트 (Adjacency List) : 링크드 리스트(or 리스트)로 그래프의 연결 관계를 표현
위의 방법들이 그래프를 표현할 수 있는 방법인데, 더 쉽게 표기하기 위해서 각 노드들에 번호를 매겨보겠다.
💡 제니를 0, 쉬지마이굥진을 1, 로제를 2, 카리나를 3 이라고 해보자.
2 ㅡ 3
|
0 ㅡ 1
1. 이를 인접 행렬 (=2차원 배열)로 나타내면 다음과 같다.
0 1 2 3
0 X O X X
1 O X O X
2 X O X O
3 X X O X
즉, 0을 기준으로 생각했을 때 0은 1과만 연결이 되어 있고 ! 자기 자신을 포함한 나머지 2, 3과는 연결되어있지 않기 때문에 X 표시를 해줬다고 이해하면 쉽다.
이걸 배열로 표현하면?
graph = [
[False, True, False, False],
[True, False, True, False],
[False, True, False, True],
[False, False, True, False]
]
2. 이번에는 인접 리스트로 표현해보자!
인접 리스트는 모든 노드에 연결된 노드에 대한 정보를 차례대로 다음과 같이 저장한다.
0 → 1
1 → 0 → 2
2 → 1 → 3
3 → 2
이걸 딕셔너리로 표현하면?
graph = {
0: [1],
1: [0, 2]
2: [1, 3]
3: [2]
}0은 1과 연결, 1은 0과 2와 연결, 2는 1과 3과 연결 ,... 이런 식으로 표현할 수 있다.
✏️두 방법의 차이
두 가지 표현 방법은 어떤 차이점이 있을까?
그래프는 주로 인접 리스트로 많이 표현을 하게 되는데, 이유는 공간 복잡도가 인접 리스트가 훨씬 적기 때문이다. 시간과 공간 복잡도 위주로 두 방법을 비교해보자.
시간 vs 공간
인접 행렬
인접 행렬로 표현하면 즉각적으로 0과 1이 연결되었는지 여부를 바로 알 수 있다.
그러나, 모든 조합의 연결 여부를 저장해야 하기 때문에 O(노드²) 만큼의 공간을 사용해야 한다. (즉, 공간 복잡도 O(N ² ))

가중치가 없는 무방향 그래프의 경우 , 두 개의 노드에서 간선이 동시에 연결되어 있기 때문에 인접 행렬이 대칭적 구조를 갖는다.
가중치가 있는 유방향 그래프에선 행렬에서 각 간선의 가중치 값이 저장되는 것을 볼 수 있다. 이 경우 가중치가 0인 것과 간선이 없는 것이 구별돼야 한다.
💡 장/단점
장점: 2차원 배열에 모든 노드들의 간선 정보가 있기 때문에, 두 노드를 연결하는 간선을 조회할 때 O(1)의 시간 복잡도를 가진다. (= 간선 탐색이 빠름!)
또한, 2차원 배열만 사용하므로 구현이 간단하다.
단점: 간선의 수와 무관하게 항상 n² 크기의 2차원 배열이 필요하므로 메모리 공간이 낭비된다. 그래프의 모든 간선의 수를 알아내려면 인접 행렬 전체를 확인해야 하므로 O(n²)의 시간이 소요된다. (= 공간 낭비 및 이웃 탐색이 비효율적)
인접 리스트
인접 리스트로 표현하면 즉각적으로 연결되었는지 알 수 없고, 각 리스트를 돌아봐야한다.
따라서 연결되었는지 여부를 알기 위해선 최대 O(간선) 만큼의 시간을 사용해야 하는데, 대신 모든 조합의 연결 여부를 저장할 필요가 없으니 O(노드 개수 + 간선 개수) 만큼의 공간을 사용하면 된다는 원리이다.
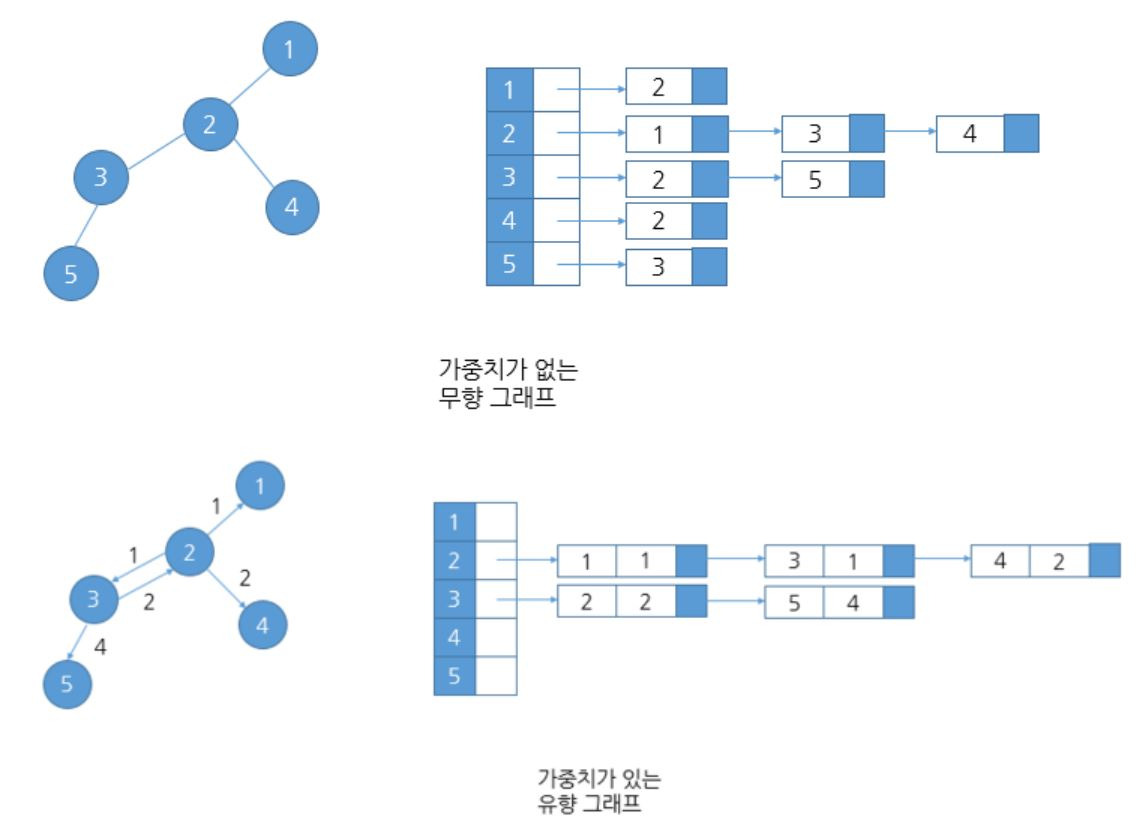
가중치가 없는 무방향 그래프는 그림과 같이 가중치 표현 없이 인접한 노드 정보가 저장되고,
가중치가 없는 유방향 그래프는 종점 [ 노드번호 | 간선의 가중치 ] 정보가 저장된다.
💡장/단점
장점: 존재하는 간선만 관리하므로 메모리 사용이 보다 효율적이다. 또한 특정 노드의 이웃 탐색 시, 해당 노드의 연결 리스트만 확인하면 되므로 이웃 탐색이 빠르다.
단점: 두 노드를 연결하는 간선을 조회하거나, 노드의 차수를 알기 위해서는 노드의 인접 리스트들을 탐색해야 하므로 노드의 차수만큼의 시간이 필요하다. (= 간선 탐색이 느림)
또한 각 노드에 연결된 리스트를 관리해야 하므로 구현이 복잡하다.
✏️인접행렬과 인접리스트의 비교
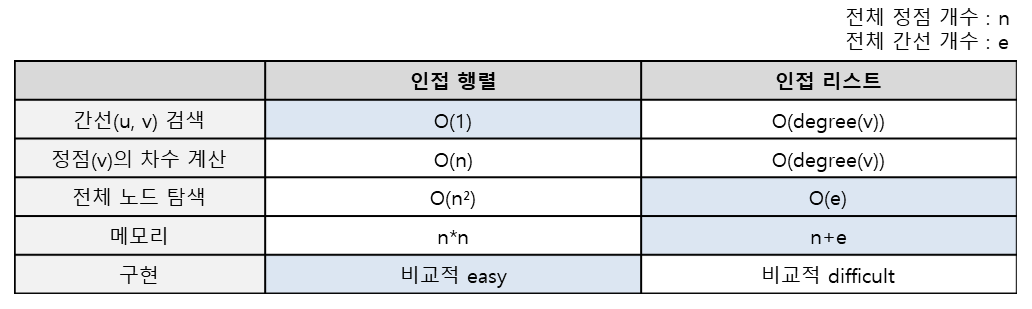
상단의 내용에서 인접 행렬과 인접 리스트를 언제 사용하면 좋을지 생각해보면.. (주로 인접 리스트로 구현하긴 하나, 인접 행렬로 구현해야 좋을 경우가 있다)
언제 사용해야 할까?
- 인접행렬을 사용해야 하는 경우:
- 그래프가 밀집 그래프(Dense Graph, 간선이 많은 경우)인 경우.
- 간선의 존재 여부를 빠르게 확인해야 하는 경우.
- 인접리스트를 사용해야 하는 경우:
- 그래프가 희소 그래프(Sparse Graph, 간선이 적은 경우)인 경우.
- 이웃 노드 탐색이 주된 작업인 경우.
그래프를 파헤쳐 봤으니 다음 포스팅에서는 그래프를 기반으로 동작하는 BFS DFS를 뿌셔봐야겠다.
'Algorithm' 카테고리의 다른 글
| [TIL][Algorithm] 다익스트라 알고리즘과 그 구현 (3) | 2024.03.29 |
|---|---|
| [Algorithm] 알고리즘 공부를 시작하며 / 알고리즘 개요 (1) | 2024.01.03 |