오늘의 스터디 주제는 알고리즘, 그 중에서도 다익스트라 알고리즘에 대해 자세히 소개하고 싶어 포스팅해본다. 처음 알고리즘을 배울 때 정렬이나 BFS, DFS같은 알고리즘들은 한 번 배우고 아, 이런 식으로 풀면 되겠구나! 가 대충 감이 왔는데, 다익스트라의 경우 감이 잘 안잡혀서 당황했던 기억이 있다.
나와 스터디원들의 감을 다시 잡아보기 위해 포스팅 야무지게 써보겠다 !!!
📌 최단 경로 (shortest path)
우선, 다익스트라 알고리즘과 함께 딸려오는 키워드가 '최단 경로'이다.
알고리즘 문제를 풀 때, 'A에서 B로 가는 최소 비용이 얼마인가?' 이런 유형을 왕왕 본 적이 있을 것이다. 보통은 이런 공간적인 문제를 그래프로 표현하고, 각 지점은 노드, 도로는 간선으로 표현이 된다.
일반적으로 최단 경로 문제에서는 각 노드는 다양한 형태로 표현될 수 있는데, 예를 들면 마을, 도시, 국가 등등으로 다르게 주어진다.
이럴 때 알고리즘은 다익스트라 혹은 플로이드-워셜 등을 이용하게 되는데, 오늘은 다익스트라가 중점이니 플로이드-워셜은 추후에 포스팅해보겠다.
실무에서는 보통 어떻게 쓰일까 ?
우리가 일반적으로 사용하는 지도 앱 등에서 굉장히 광범위하게 사용이 되고 있다!!
그럼 지도 앱에서 최단 경로를 구현해야 할 때 쓰는 다익스트라 알고리즘은 뭐고 어떻게 구현하는지 제대로 배우러 가보자.
다양한 문제 상황
- 한 지점에서 다른 한 지점까지의 최단 경로
- 한 지점에서 다른 모든 지점까지의 최단 경로
- 모든 지점에서 다른 모든 지점까지의 최단 경로
📌다익스트라 알고리즘이란 ?
개요
일단 다익스트라 알고리즘은 '다익스트라'가 만들어서 다익스트라라고 이름이 붙었다.

다익스트라 알고리즘을 한 줄로 정리하면,
"출발점이 정해져 있을 때, 나머지 모든 노드에 이르는 최소 비용을 계산하는 알고리즘"이다.
다익스트라 최단 경로 알고리즘은 음의 간선이 없을 때 정상적으로 동작한다. (현실 세계의 도로 (간선)은 음의 간선으로 표현되지 않기 때문에 길 찾기 등에서 활용될 수 있는 것)
또한 매 상황에서 가장 비용이 적은 노드를 선택해 임의의 과정을 반복하므로 그리디 알고리즘으로 분류된다.
하단의 이미지가 다익스트라 알고리즘을 설명하는 기본적인 도표라고 보면 된다.

위의 도표에서는 출발 지점이 s, 다른 노드들은 t, x, y, z 로 정해져 있다. 이 때 노드 사이 간선에 써 있는 숫자가 각 노드에 이르기까지의 최소 비용이라고 보면 된다. (a)단계 부터 (f)단계까지 차근차근 설명을 해보겠다.
(a)
시작이 s 라고 했을 때, 일단 모든 노드에 이르는 비용을 ∞ (무한대)로 기록하고 시작한다.
출발지를 기준으로 인접 노드를 살펴본다. (바로 갈 수 있는 노드들)
살펴봤더니 t는 10의 비용으로, y는 5의 비용으로 갈 수 있다. 그럼 각각 기존에 기록해 둔 최소 비용과 비교를 해보는거다.
t와 y 모두 ∞ 로 기록해두고 있다. 업데이트를 해주자.
(b)
t와 y의 최소 비용을 ∞ 에서 👉 10과 5로 업데이트 해줬다.
그리고 s에 대해서는 다 했다! 라고 표시를 해준다. (해당 도표에서는 까만 색칠 표시)
그 다음 나머지 모든 노드에 대해서 가장 비용이 적은 놈을 고른다.
(a)에서 t의 최소비용을 10으로 업데이트 해 줬지만, y → t의 최소비용이 5+3 = 8이므로 8로 업데이트를 해준다.
(c)
t의 최소 비용을 10에서 👉 8로 업데이트 해 준 후, y → x 도 생각해본다.
x의 최소비용이 원래는 ∞ 였지만, 5+9 = 14 이므로 ∞ 에서 👉 14로 업데이트 해준다.
y → z 도 생각해보자. 원래는 ∞ 였지만, 5+2 = 7 이므로 ∞ 에서 👉 7로 업데이트 해준다.
인접 노드들에 대해서 처리가 끝났으므로 y에 대해서도 다 했다! 는 의미로 방문 처리(까만 색칠 표시)를 해준다.
나머지 t, x, z 노드에 대해서도 최소 비용을 구해보자. 8, 14,7 중 7이 제일 작기 때문에 7부터 시작한다.
인접 노드를 보면 방문 처리 하지 않은 곳은 x 밖에 없다. x는 원래 14지만 z → x 는 7+6 = 13이므로, 14 에서 👉 13으로 업데이트 해준다.
처리가 끝났으므로 z 노드에 대해서도 방문 처리를 해주자.
(d)
나머지 t, x 노드에 대해서 최소 비용을 구하자. 8, 13 중 작은 8(t)부터 시작한다.
t 를 기준으로 인접 노드는 x와 y가 있다.
t → x 는 원래는 13이지만, 8+1 = 9 이므로 13 에서 👉 9로 업데이트 해준다.
t → y 는 원래는 5이지만, 8+2 = 10 이므로 더 작은 숫자가 아니므로 업데이트 없이 그대로 내버려둔다.
처리가 끝났으므로 t 노드에 대해서도 방문 처리를 해주자.
(e)
마지막으로 남은 x (9)노드를 생각해보자. x를 기준으로 자식 노드는 z가 있다.
x → z 는 원래는 7이지만, 9+4 = 13 이므로 더 작은 숫자가 아니므로 업데이트 없이 그대로 내버려둔다.
(f)
(e)에서 x에 대해 방문처리를 해주면 최종 (f)의 도표가 된다!
결과는 0, 8, 9, 5, 7 이 된다.
위의 순서를 코드로 하면 이와 가깝게 될 것이다.
1. 출발지를 s로 정하고, 다음과 같이 표시한다.
(s, t, x, y, z 순)
거리 = [0, inf, inf, inf, inf]
방문 = [True, False, False, False, False]
2. 갈 수 있는 노드들의 최소거리를 측정한다.
s->t: 10
s->y: 5
(s, t, x, y, z 순)
거리 = [0, 10, inf, 5, inf]
방문 = [True, False, False, False, False]
3. 방문 안한 녀석들 중 가장 가까운 녀석인 y를 방문하고, 최소거리를 측정한다.
y->t: 3
y->x: 9
y->z: 2
(s, t, x, y, z 순)
거리 = [0, 8, 14, 5, 7]
방문 = [True, False, False, True, False]
4. 방문 안한 녀석들 중 가장 가까운 녀석인 z를 방문하고, 최소거리를 측정한다.
z->x: 6
(s, t, x, y, z 순)
거리 = [0, 8, 13, 5, 7]
방문 = [True, False, False, True, True]
5. 방문 안한 녀석들 중 가장 가까운 녀석인 t를 방문하고, 최소거리를 측정한다.
t->x: 1
t->y: 2
(s, t, x, y, z 순)
거리 = [0, 8, 9, 5, 7]
방문 = [True, True, False, True, True]
6. 방문 안한 녀석들 중 가장 가까운 녀석인 x를 방문하고, 최소거리를 측정한다.
x->z: 4
(s, t, x, y, z 순)
거리 = [0, 8, 9, 5, 7]
방문 = [True, True, True, True, True]
7. 방문 안한 노드가 없으므로 끝낸다.
(s, t, x, y, z 순)
거리 = [0, 8, 9, 5, 7]
방문 = [True, True, True, True, True]- 거리는 숫자로 표시, 방문 여부는 True, False로 표시
- 결과는 0, 8, 9, 5, 7로 동일하게 나옴
- 1~3번 과정이 반복된다고 보면 됨
이것이 기본적인 다익스트라 알고리즘의 구조다.
📌 다익스트라 알고리즘 구현
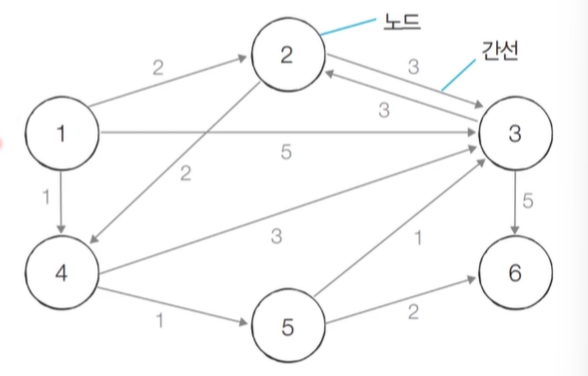

출발지가 1일 때, 1까지 가는 비용은 0, 6까지 가는 비용은 4 라는 내용의 테이블이 만들어진다. 이 내용을 직접 구현해보자!
6 11
1
1 2 2
1 3 5
1 4 1
2 3 3
2 4 2
3 2 3
3 6 5
4 3 3
4 5 1
5 3 1
5 6 2
testcase1.txt
이 테스트 케이스는 상단의 그래프를 표현하고 있는 테스트 케이스이다. (6은 노드의 갯수, 11은 간선의 갯수, 1은 출발지)
우리가 원하는 것은 결과값으로 상단의 배열 표가 나오는 것!
import sys
from min_cost.dijkstra import dijkstra_naive, dijkstra_pq
with open('testcase1.txt') as f:
sys.stdin = f
input = sys.stdin.readline
n, m = map(int, input().split())
start = int(input())
graph = [[] for _ in range(n + 1)]
for _ in range(m):
a, b, c = map(int, input().split())
graph[a].append((b, c))
assert dijkstra_naive(graph, start) == [1000000000, 0, 2, 3, 1, 2, 4]상단의 테스트케이스를 통해서 n, m, start를 입력 받고, graph(빈 배열)를 만든 다음, graph를 기준으로 graph의 a번째에 튜플을 저장 (b: 목적지, c: 비용) 한다.
이 때 다익스트라를 나이브하게 구현한 버전의 결과값을 보면 0, 2, 3, 1, 2, 4 로 상단의 표와 일치하는 것을 볼 수 있다. (배열의 0번째 노드는 없기 때문에 무시)
그럼 dijkstra_naive 함수는 어떻게 구현해야 할지 코드를 보자.
INF = int(1e9) # 무한을 의미하는 값으로 10억을 설정
def dijkstra_naive(graph, start):
# 방문하지 않은 노드 중에서, 가장 최단 거리가 짧은 노드의 번호를 반환
def get_smallest_node():
min_value = INF
idx = 0 # 가장 최단 거리가 짧은 노드 (인덱스)
for i in range(1, N):
if dist[i] < min_value and not visited[i]:
min_value = dist[i]
idx = i
return idx
N = len(graph)
visited = [False] * N
dist = [INF] * N
visited[start] = True
dist[start] = 0
for adj, d in graph[start]:
dist[adj] = d
# N개의 노드 중 첫 노드는 이미 방문했으므로,
# N-1번 수행하면 된다.
for _ in range(N - 1):
# 가장 가깝고 방문 안한 녀석을 고르고, 방문 처리
cur = get_smallest_node()
visited[cur] = True
# 최단거리를 비교, 수정한다.
for adj, d in graph[cur]:
cost = dist[cur] + d
# 현재 노드를 거쳐서 다른 노드로 이동하는 거리가 더 짧은 경우
if cost < dist[adj]:
dist[adj] = cost
return dist1. visited(방문 여부) 와 dist(거리) 배열을 그래프의 길이 만큼 만든다.
2. 출발 부분은 방문처리 해주고 거리는 0으로 잡는다.
3. 갈 수 있는 노드들의 최소 거리를 측정해준다. adj: 인접 노드, d: 그곳으로 가는 비용
최종적으로 원하는 최단 거리 배열의 인접 노드로 가는 비용을 d로 업데이트 해준다. (dist[adj] = d)
이 과정은
2. 갈 수 있는 노드들의 최소거리를 측정한다.
s->t: 10
s->y: 5
(s, t, x, y, z 순)
거리 = [0, 10, inf, 5, inf]
방문 = [True, False, False, False, False]이 과정과 같다.
4. 가장 가깝고 방문 하지 않은 녀석을 고르고, 방문 처리를 해 준 다음, 최단 거리를 비교 & 수정한다.
이 과정은
3. 방문 안한 녀석들 중 가장 가까운 녀석인 y를 방문하고, 최소거리를 측정한다.
y->t: 3
y->x: 9
y->z: 2
(s, t, x, y, z 순)
거리 = [0, 8, 14, 5, 7]
방문 = [True, False, False, True, False]이 부분과 같고, 이후 방문 하지 않은 노드가 없을 때까지 이 3번을 계속 반복하는 것이다.
위 코드는 이중 for 문이므로 O(N^2)의 시간 복잡도를 가진다.
= O(V^2) (V는 노드의 개수를 의미)
일반적으로 코딩 테스트의 최단 경로 문제에서 전체 노드의 개수가 5,000개 이하라면 이 코드로 문제를 해결할 수 있다. (파이썬 기준)
하지만 노드의 개수가 10,000개를 넘어가는 문제라면?
위 코드에서 줄일 수 있는 부분을 줄여 시간 복잡도를 개선하려면 어떻게 해야할까?
위 dijkstra_naive 함수의 get_smallest_node() 메서드를 조금 더 효율적으로 만들 수 있지 않을까?
get_smallest_node 메서드는 지금까지 도달비용이 제일 작으면서, 방문 안 한 노드를 가져오는 메서드이다.
'가장 작은' 값을 꺼낸다 라고 생각했을 때, 생각나는 것은?!
Heap
바로 힙! 힙을 써서 위 메서드를 효율적으로 리팩토링 할 수 있다.
힙 중에서 최소 힙을 쓰면, 원래 get_smallest_node() 의 시간복잡도를 O(N) 👉 O(logN) 으로 줄일 수 있다.
아이디어 :
파이썬에는 기본적으로 최소힙이 구현돼서 내장 돼 있다.
아래 코드는 *우선순위 큐 개념을 힙을 사용해서 구현한 dijkstra_pq 함수이다.
* 우선순위 큐 (Priority Queue) 란? 선입선출이라는 큐의 특성과는 조금 다르게, 내부적으로 정해진 어떤 규칙에 의해서 각 요소의 우선순위가 결정되게 되고, 우선순위가 가장 높은 녀석부터 제일 먼저 나간다는 개념
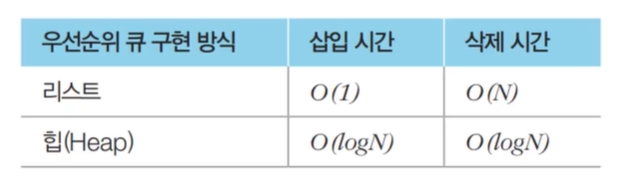
즉, 힙 또한 결국 최대냐 최소냐 내부 규칙에 의해서 한 요소를 지속적으로 꺼내는 것이기 때문에 우선순위 큐와 결이 비슷하다고 할 수 있다.
개선된 구현 방법
기본 원리는 동일하나, 현재 가장 가까운 노드를 저장해 놓기 위해서 힙 자료구조를 추가적으로 이용한다는 점이 다르다.
현재의 최단 거리가 가장 짧은 노드를 선택해야 하므로 최소 힙을 사용한다.
import heapq
def dijkstra_pq(graph, start):
N = len(graph)
dist = [INF] * N
q = []
# 시작 노드로 가기 위한 최단 거리는 0으로 설정하여, 큐에 삽입
heapq.heappush(q, (0, start))
dist[start] = 0
while q: # 큐가 비어있지 않다면
# 누적 비용이 가장 작은 녀석을 꺼낸다.
acc, cur = heapq.heappop(q)
# 현재 노드가 이미 처리된 적이 있는 노드라면 무시
if dist[cur] < acc:
continue
# 인접 노드를 차례대로 살펴보며 거리를 업데이트한다.
for adj, d in graph[cur]:
cost = acc + d
# 현재 노드를 거쳐서, 다른 노드로 이동하는 거리가 더 짧은 경우
if cost < dist[adj]:
dist[adj] = cost
heapq.heappush(q, (cost, adj))
return dist1. 거리를 무한대(inf)로 세팅 해 준다. (기본적으로 visited 는 필요 없다)
2. heappush로 방문하지 않는 노드 값으로 튜플을 넣어주면서 시작한다. (0, start)
3. 그 다음 거리를 0으로 처리 해준다.
4. 노드가 있는 동안은 이 과정을 계속 반복 해준다. (while문)
import sys
from min_cost.dijkstra import dijkstra_naive, dijkstra_pq
with open('testcase1.txt') as f:
sys.stdin = f
input = sys.stdin.readline
n, m = map(int, input().split())
start = int(input())
graph = [[] for _ in range(n + 1)]
for _ in range(m):
a, b, c = map(int, input().split())
graph[a].append((b, c))
assert dijkstra_naive(graph, start) == [1000000000, 0, 2, 3, 1, 2, 4]
assert dijkstra_pq(graph, start) == [1000000000, 0, 2, 3, 1, 2, 4]
시간복잡도 비교
Naive 하게 구현 : O(V^2)
PriorityQueue로 구현 : O(ElogV) (E (edge) : 간선, V (vertex) : 정점)
📌 동작 과정 정리
- 출발 노드를 설정한다.
- 최단 거리 테이블을 초기화한다. (노드까지 가기 위한 비용은 무한으로, 자기 자신에 대한 비용은 0으로 설정)
- 방문하지 않은 노드 중에서 최단 거리가 가장 짧은 노드를 선택한다.
- 해당 노드를 거쳐 다른 노드로 가는 비용을 계산해서 최단 거리 테이블을 갱신한다.
- 위 과정에서 3번과 4번을 반복한다.
'Algorithm' 카테고리의 다른 글
| [TIL][자료구조] 그래프의 개념과 표현 방법 (2) | 2024.12.02 |
|---|---|
| [Algorithm] 알고리즘 공부를 시작하며 / 알고리즘 개요 (1) | 2024.01.03 |