알고리즘 문제를 풀다 최소 공배수를 구해야 하는 문제를 맞닥뜨렸다.
필자는 for문으로 풀었지만, 풀고 난 후 다른 적합한 풀이 방법이 있나 찾아보다 파이썬에서 최소 공배수를 구하는 함수가 있다는 걸 알았다. 공유도 하고 잊지 않고 다음에 써먹기도 할 겸 포스팅한다 🍀
✏️ 최소 공배수란?
먼저 다들 알고 있겠지만 최소 공배수가 뭔지 간단히 짚고 넘어가보려 한다.
최소 공배수(LCM, Least Common Multiple)는 두 수의 배수 중에서 가장 작은 공통 배수를 의미한다. 예를 들어, 4와 6의 최소 공배수는 12 이다.
개념
최소 공배수는 다음과 같은 특성을 가지고 있다.
- 두 수의 공통된 배수 중 가장 작은 수
- 최소 공배수를 구하기 위해 최대 공약수(GCD, Greatest Common Divisor)를 사용
수학적 정의
우리가 중학교 시절 풀었던 식은 이렇다. 두 수 12와 18의 최소 공배수를 구하는 방법:
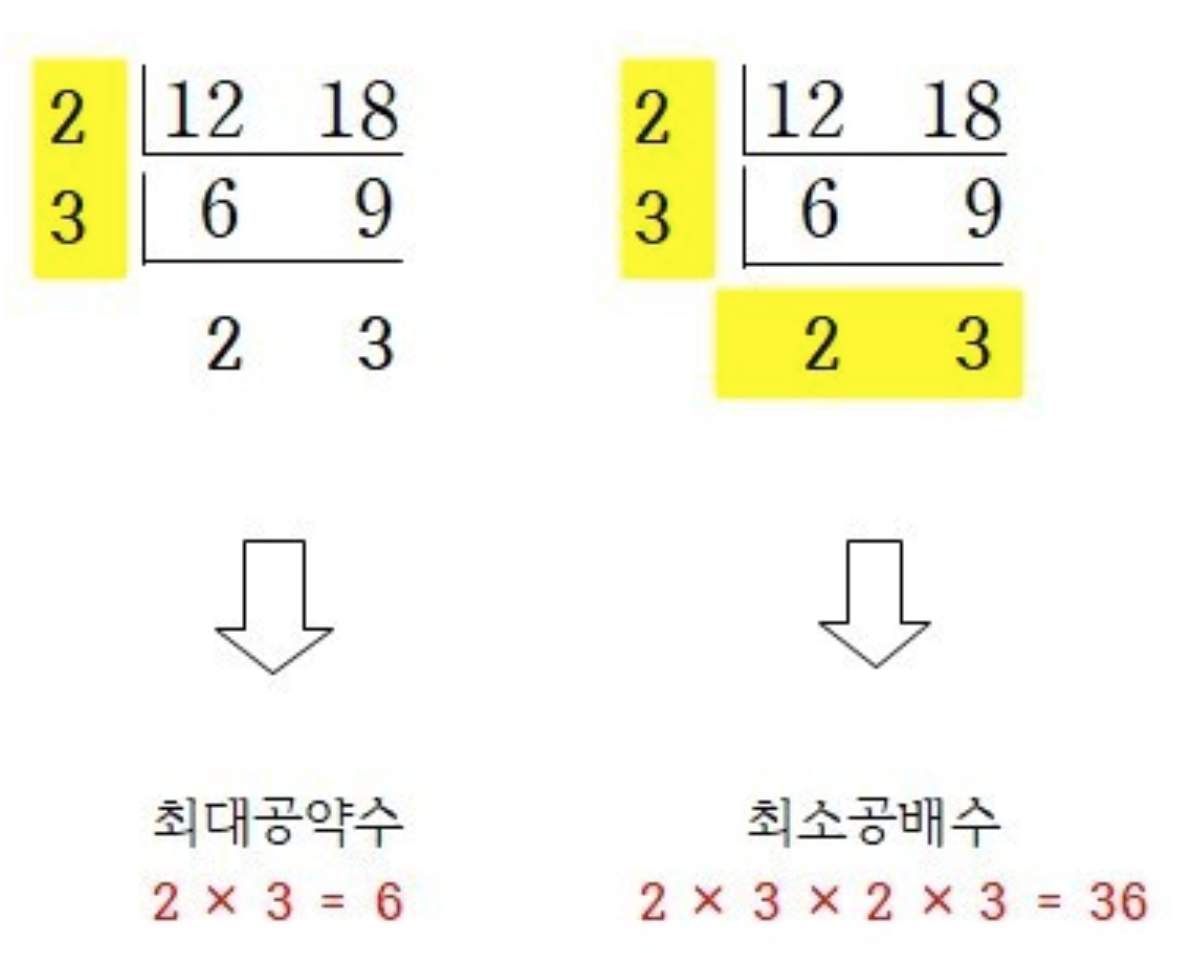
이 방법을 식으로 만들면 이렇다.
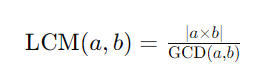
여기서 GCD(a, b)는 a와 b의 최대 공약수를 의미한다.
✏️ Python에서 최소 공배수 구하기
Python의 math 모듈을 사용하면 위의 식을 바탕으로 최대 공약수를 쉽게 구할 수 있다. (두둥 ..) 이 모듈을 활용해서 최소 공배수를 쉽게 구해보자.
코드 예제
먼저 math.gcd 함수를 사용하여 a와 b의 최대 공약수를 구할 수도 있다.

이제 이를 바탕으로 최소 공배수를 계산해보자.

위 코드에서 lcm 함수의 동작 방식을 설명해보면,
- a와 b의 곱을 구한다. (abs 함수를 사용해서 결과가 항상 양수가 되도록 보장)
- a와 b의 최대 공약수로 나눈다.
- 그 결과를 반환한다.
math.gcd 함수를 알았으니 ,, 최대 공약수 뿐만 아니라 최소 공배수까지 구할 수 있어 복잡한 문제에 써먹을 수 있을 것 같다. 까먹지말고 다음에 써먹자 !!
코드
import math
def lcm(a, b):
return abs(a * b) // math.gcd(a, b)
# 두 수의 최소 공배수 구하기
a = 12
b = 18
result = lcm(a, b)
print(f"{a}와 {b}의 최소 공배수: {result}")'Programming Languages > Python' 카테고리의 다른 글
| [Python] zip과 dict로 리스트 2개 딕셔너리로 매핑하기 (feat. for문 탈출) (3) | 2024.12.17 |
|---|---|
| [Python] 파이썬에서의 집합, set 함수 (5) | 2024.08.12 |
| [Python] 리스트 append 와 extend의 차이 (2) | 2024.05.14 |
| [Python] 알고리즘 문제 풀다 발견한 대소문자 바꾸기 메서드.. 우리의 시간을 아끼자 ^ㅡ^ (1) | 2024.05.13 |
| [Python] 리스트와 딕셔너리의 차이 (3) | 2024.04.29 |