프로그래머스에서 문제를 풀다가, 나의 경우 for문으로 풀었던 문제를 다른 사람은 set 함수로 간단히 푼 것을 보고 set 함수를 자세히 찾아보게 되었다. 포스팅 하면서 set 함수의 사용법과 쓰임에 대해 까먹지 않으려고 (!!!) 포스팅해본다.
SET 함수란?
자바의 set 함수와 같이, 파이썬의 set 함수 또한 집합을 생성하기 위해 사용된다.
집합은 '중복되지 않는 요소들의 모음'으로, 수학에서의 집합을 생각하면 되고! 파이썬의 set 함수는 집합 연산(합집합, 교집합, 차집합 등)을 지원한다는 것 까지 알아두자.
기본 사용법
# 빈 집합 생성
s = set()
# 리스트나 문자열 등을 사용해 집합 생성
s = set([1, 2, 3, 4, 4])
print(s) # 출력: {1, 2, 3, 4} # 중복된 4가 제거됨
s = set("hello") # 문자열을 집합으로 변환 (중복된 'l'이 제거됨)
print(s) # 출력: {'h', 'e', 'l', 'o'}코드를 보면 이해가 쉽다. 리스트 형태로도 집합을 만들 수 있고, 문자열 또한 집합으로 만들어줄 수 있다 !!!
집합의 특성
- 중복 허용 안 함:
- set은 같은 값을 중복해서 저장하지 않는다.
- ex) [1, 2, 2, 3]을 집합으로 변환하면 {1, 2, 3}이 된다.
- 순서가 없음:
- 집합은 순서가 없으므로 인덱싱(indexing)이 불가능하다.
- 요소의 순서가 의미가 없으며, 저장된 순서대로 출력되지 않을 수 있다.⭐ (순서 보장 불가!)
- 수학적 집합 연산 지원:
- set은 합집합, 교집합, 차집합 등을 지원한다.
- set은 합집합, 교집합, 차집합 등을 지원한다.
- 빠른 연산:
- set은 요소의 존재 여부를 매우 빠르게 확인할 수 있다. in 연산의 시간 복잡도는 O(1) 이다.
- 이로 인해 큰 데이터셋을 다룰 때 유용하다.
a = set([1, 2, 3, 4])
b = set([3, 4, 5, 6])
print(a | b) # 합집합: {1, 2, 3, 4, 5, 6}
print(a & b) # 교집합: {3, 4}
print(a - b) # 차집합: {1, 2}
print(a ^ b) # 대칭 차집합(양쪽에만 있는 요소들): {1, 2, 5, 6}
<빠른 연산 예제>
s = set([1, 2, 3, 4, 5])
print(3 in s) # 출력: True
print(6 in s) # 출력: False
사용 예시
# 중복된 요소 제거
numbers = [1, 2, 2, 3, 4, 4, 5]
unique_numbers = set(numbers)
print(unique_numbers) # 출력: {1, 2, 3, 4, 5}
# 리스트로 다시 변환
unique_list = list(unique_numbers)
print(unique_list) # 출력: [1, 2, 3, 4, 5]
# 집합 연산 예시
set_a = set([1, 2, 3])
set_b = set([3, 4, 5])
print(set_a.union(set_b)) # 합집합: {1, 2, 3, 4, 5}
print(set_a.intersection(set_b)) # 교집합: {3}프로그래머스 문제풀이에 사용
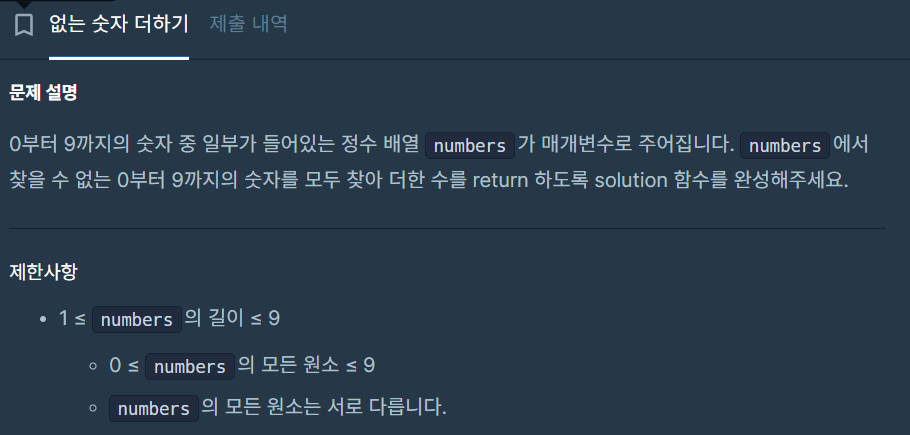
오늘 풀어본 문제였다.
1차 풀이 (for문 사용) 👉 정답
def solution(numbers):
num_list = [0, 1, 2, 3, 4, 5, 6, 7, 8, 9]
answer = 0
for i in num_list:
if i not in numbers:
answer += i
return answer
num_list를 순회하면서 numbers 배열에 없는 숫자를 찾고, if i not in numbers:를 사용하여 numbers에 없는 숫자를 answer에 더한 후 answer를 반환하는 간단한 코드이다.
시간 복잡도의 경우는 O(N * M)이 된다(N은 num_list의 길이, M은 numbers의 길이). num_list는 10개로 한정되어 있으니 정확히는 O(10 * M)일 것이다.
2차 풀이 (set 함수 사용) 👉 정답
def solution(numbers):
return sum(set(range(10)) - set(numbers))
- range(10): 0부터 9까지의 숫자를 생성한다.
- set(numbers): 주어진 numbers 리스트를 집합으로 변환한다.
- 차집합 연산: set(range(10)) - set(numbers)는 0부터 9까지의 집합에서 numbers 집합을 뺀 결과를 반환한다.
- sum() 함수: 차집합으로 남은 숫자들의 합을 계산한다.
시간복잡도는 O(1)이 된다. range(10)은 상수 크기의 집합을 생성하고, numbers 배열의 크기가 최대 9 이므로 for문을 사용한 풀이와 비교하면 매우 빠른 연산이다.
마치며
알고리즘 문제를 풀면서 알게 된 set 함수를 자세히 학습해봤다. 이렇게 짠 코드가 성능 측면에서도 우수하고, 코드가 더 간결해져 가독성 또한 더 좋아서 비슷한 류의 문제를 풀 때는 set 함수를 잊지말고 써봐야겠다.
'Programming Languages > Python' 카테고리의 다른 글
| [Python] Python3와 PyPy3의 차이 (2) | 2024.12.19 |
|---|---|
| [Python] zip과 dict로 리스트 2개 딕셔너리로 매핑하기 (feat. for문 탈출) (3) | 2024.12.17 |
| [Python] 파이썬에서 최소 공배수 함수로 구하기 (1) | 2024.06.13 |
| [Python] 리스트 append 와 extend의 차이 (2) | 2024.05.14 |
| [Python] 알고리즘 문제 풀다 발견한 대소문자 바꾸기 메서드.. 우리의 시간을 아끼자 ^ㅡ^ (1) | 2024.05.13 |